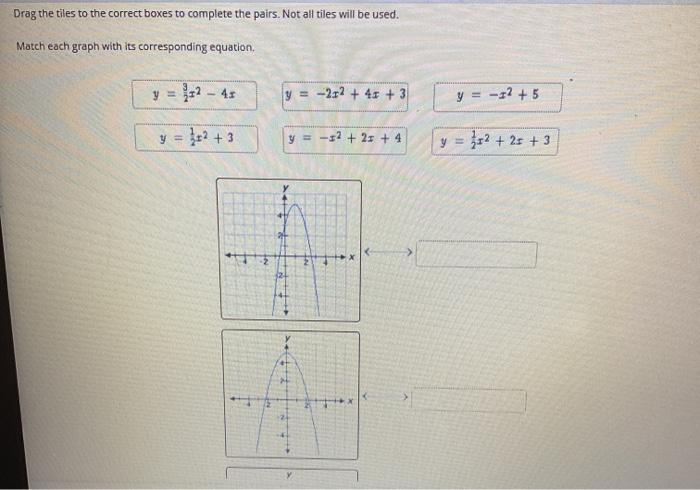
Match each graph with the quadratic function it represents – Matching each graph with the quadratic function it represents is a fundamental skill in understanding the relationship between algebraic and geometric representations of quadratic functions. This interactive activity provides a comprehensive approach to grasping this concept, fostering a deeper understanding of the characteristics and properties of quadratic functions.

Through a combination of theoretical explanations, practical examples, and interactive exercises, this guide will equip learners with the knowledge and skills to confidently match graphs to their corresponding quadratic functions.

1.

Identify Quadratic Functions

Quadratic functions are polynomial functions of degree 2, which means they have a term with the square of the independent variable. The general form of a quadratic function is f(x) = ax^2 + bx + c, where a, b, and c are real numbers and a is not equal to 0.Quadratic

functions can be written in various forms, including:

Standard form

f(x) = ax^2 + bx + c

Factored form

f(x) = a(x

• r)(x
• s), where r and s are the roots of the function

Vertex form

f(x) = a(x

• h)^2 + k, where (h, k) is the vertex of the parabola

Quadratic functions have several characteristic features:

Vertex

The vertex is the point where the parabola changes direction. The x-coordinate of the vertex is given by h =b/2a, and the y-coordinate is given by k = f(h).

Axis of symmetry

The axis of symmetry is a vertical line that passes through the vertex. The equation of the axis of symmetry is x = h.

Intercepts

The intercepts are the points where the parabola intersects the x- and y-axes. The x-intercepts are found by solving f(x) = 0, and the y-intercept is found by evaluating f(0).

2.

Matching Graphs and Functions

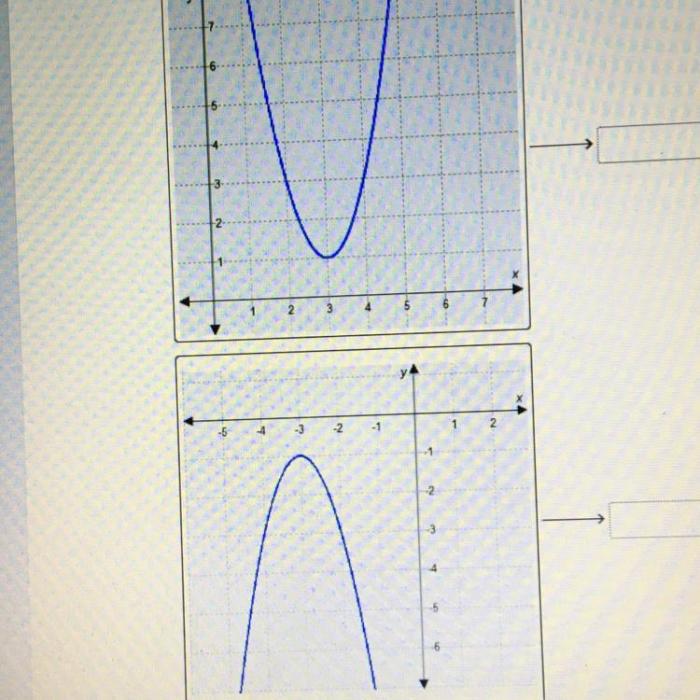
The graph of a quadratic function is a parabola. The shape of the parabola depends on the values of a, b, and c. If a > 0, the parabola opens upward, and if a < 0, the parabola opens downward. The vertex of the parabola is the point where it changes direction. To match a graph to its corresponding quadratic function, follow these steps: 1. Determine the vertex of the parabola. 2. Determine whether the parabola opens upward or downward. 3. Use the vertex and the direction of opening to determine the sign of a. 4. Find the x-intercepts of the parabola. 5. Use the x-intercepts to determine the values of b and c. The importance of key features (e.g., vertex, intercepts) in matching graphs and functions is that they provide information about the shape and location of the parabola. The vertex tells us where the parabola changes direction, and the x-intercepts tell us where the parabola intersects the x-axis. This information can be used to narrow down the possible quadratic functions that could match the graph.

Frequently Asked Questions: Match Each Graph With The Quadratic Function It Represents

What is the purpose of matching graphs with quadratic functions?

Matching graphs with quadratic functions helps individuals visualize the relationship between the algebraic and geometric representations of quadratic functions. It enhances their understanding of the key features of quadratic functions, such as the vertex, axis of symmetry, and intercepts.

How can I use this interactive activity to improve my understanding of quadratic functions?

This interactive activity provides a step-by-step approach to matching graphs with quadratic functions. By working through the examples and exercises, you can develop a deeper understanding of the characteristics of quadratic functions and their graphical representations.

What are the benefits of using an interactive table for matching graphs and functions?

An interactive table allows you to visualize the relationship between different quadratic functions and their graphs in a clear and organized manner. It facilitates the comparison of key features and provides a structured approach to matching graphs with their corresponding functions.