Evaluate the integral by changing to cylindrical coordinates – Evaluating integrals using cylindrical coordinates is a valuable technique that offers a powerful approach to solving complex integrals. By converting integrals from rectangular coordinates to cylindrical coordinates, we unlock a simplified method for evaluating integrals, particularly those involving circular or cylindrical shapes.
This article delves into the concept of cylindrical coordinates, explains the procedure for converting and evaluating integrals, and explores the diverse applications of cylindrical coordinates in various fields.
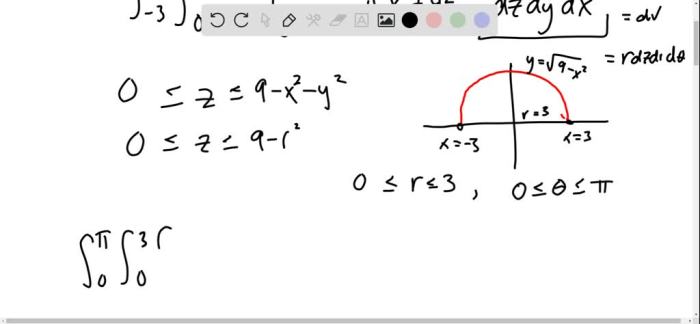
Define Cylindrical Coordinates: Evaluate The Integral By Changing To Cylindrical Coordinates
Cylindrical coordinates are a three-dimensional coordinate system that uses three coordinates to specify the location of a point in space: radial distance from the origin, angle from the positive x-axis, and height above or below the xy-plane.
The radial distance is denoted by r, the angle is denoted by θ, and the height is denoted by z. The relationship between cylindrical and rectangular coordinates is given by:
- x = r cos(θ)
- y = r sin(θ)
- z = z
Evaluate Integrals in Cylindrical Coordinates

To evaluate an integral in cylindrical coordinates, we first need to convert the integral from rectangular coordinates to cylindrical coordinates. This is done by substituting the expressions for x, y, and z in terms of r, θ, and z into the integral.
Once the integral has been converted to cylindrical coordinates, we can evaluate it using the following steps:
- Integrate with respect to z from z = 0 to z = h.
- Integrate with respect to θ from θ = 0 to θ = 2π.
- Integrate with respect to r from r = 0 to r = R.
Applications of Cylindrical Coordinates
Cylindrical coordinates are used in a wide variety of applications, including:
- Physics: Cylindrical coordinates are used to solve problems in electromagnetism, fluid dynamics, and heat transfer.
- Engineering: Cylindrical coordinates are used to design and analyze cylindrical objects, such as pipes, shafts, and gears.
- Mathematics: Cylindrical coordinates are used to solve problems in calculus, differential equations, and geometry.
Tips and Tricks for Evaluating Integrals in Cylindrical Coordinates
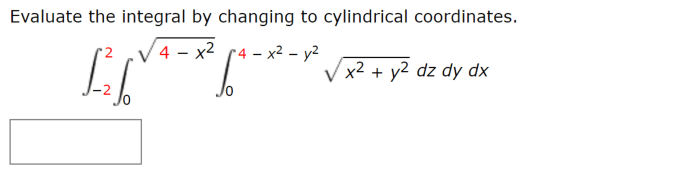
Here are a few tips and tricks for efficiently evaluating integrals in cylindrical coordinates:
- Use symmetry to reduce the limits of integration.
- Use the fact that sin(θ + π) = -sin(θ) and cos(θ + π) = -cos(θ) to simplify integrals.
- Use the following identities to convert between rectangular and cylindrical coordinates:
- r^2 = x^2 + y^2
- tan(θ) = y/x
FAQ Section
What are the advantages of using cylindrical coordinates?
Cylindrical coordinates simplify the evaluation of integrals involving circular or cylindrical shapes, making them particularly useful in physics and engineering.
When should I use cylindrical coordinates instead of rectangular coordinates?
Cylindrical coordinates are most beneficial when dealing with integrals that involve circular or cylindrical shapes, as they allow for a more straightforward evaluation process.